Linear equations are one of the most commonly tested parts of the Math sections of the SAT and ACT. Questions about lines can cover any difficulty level, from straightforward questions about slopes and intercepts to complicated questions that require us to apply linear functions to real-world problems.
Let’s jump into an application of linear equations: solving for multiple variables in a multi-equation system. First, let’s check out this sample SAT question:
This is a very common question type in which we are given the equations of two lines and are asked which coordinate pair satisfies both equations. If you see a question like this on the SAT or ACT, there are a few different techniques that will get you the correct solution. We’ll look at each, and you can choose which one to use on future questions.
Desmos
If you're taking either the SAT or the digital ACT, the easiest method by far is to use the Desmos graphing calculator built into your testing platform. Start by simply entering the two equations into Desmos.
Note that we don't need to rearrange the equations into any specific format; we can just type them in as they're presented in the question. Here's the resulting graph:
The solution to the system of equations is the point where the two lines intersect. If we click on the point, Desmos will give us its exact coordinates:
The solution is therefore (2, 7), and the correct answer is choice B, easy peasy! This method also works to solve systems of quadratic equations.
Substitution
If you're taking the paper version of the ACT, you can also use the technique above on a personal graphing calculator. However, if you only have access to a scientific or four-function calculator, another technique is the substitution method. Here, we pick one equation and solve for a variable. Let's take the second equation and solve for y.
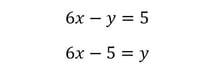
Note: you should recognize this as the equation of a line in slope-intercept form. (Quiz yourself: what are the slope and y-intercept of this line?)
Next, we go back to the first equation, and wherever we see “y”, we substitute “6x – 5”. This gives us one equation in one variable:
We’re almost there. To find y, we simply plug x=2 back in to either of the two equations:
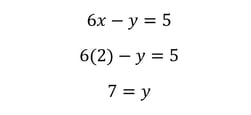
With x being equal to 2 and y being equal to 7, our answer is (2, 7), or (B).
Elimination
The final technique for solving these problems, if you don't have access to Desmos, is the elimination method. The goal of the elimination method is the same as that of the substitution method: to manipulate the equations so that we have one equation in one variable. But the elimination method does this in a much different way.
Take a look at the original two equations from the problem. Notice that the coefficient in front of the two x terms is the same: 6. In this case, we can subtract the entire second equation from the first equation, eliminating the x terms:
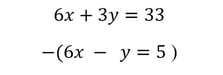
Next, we simply subtract each term from the second equation from the first. 6x — 6x = 0, so the x terms are eliminated. 3y — (–y) = 4y, and 33 — 5 = 28.
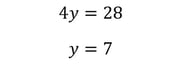
The final step is the same as in the substitution method. We choose either equation and substitute y = 7, again finding that our correct answer is (2, 7).
Once you’ve mastered the basics, you’ll be able to apply them to a variety of problems. When you’re asked to find the coordinate pair that satisfies both equations, use whichever technique—substitution or elimination—you’re more comfortable with.
For more tips, download our guide to the 6 skills you need to master for the SAT and the 6 skills you need to master for the ACT.
Need more individualized advice?
The recommendations above are general suggestions. If you have specific questions about your individual test prep plans, reach out to our experts here. We’re happy to help in any way we can.
Related Posts
How To Answer Unit Conversion Questions on the SAT Math Section
How To Answer Percentage Questions on the ACT Math Section
About ArborBridge
ArborBridge is the global leader in innovative, digital, one-on-one tutoring. With nearly a decade of experience teaching students online, ArborBridge supports students of all kinds: home schoolers, AP students, test preppers, and more. Our tutors specialize in creating personalized plans and in providing compassionate support for students and families.
