Today we move to the Math section of the ACT and look at a more specific problem type: percentage questions. While most students probably think that they have a pretty good feel for percentage questions—after all, we use percentages in our day-to-day lives—the ACT has a few tricky ways of testing percentages.
Let’s start, as usual, with a definition. “Per cent” means “per one hundred” or “out of one hundred.” The math symbol that we use for this is a fraction with 100 in the denominator. So the phrase “75% of 80 is equal to 60” would be presented like this:
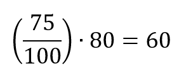
Seems easy enough so far. One of the trickier ways in which the ACT likes to test this topic is through what I call “compounded percentage growth.” Let’s take a look at a sample question:
- At the end of 1990, Jordan’s best shot put was 20 feet. At the end of 1991, he had increased his best shot put by 20%. At the end of 1992, he increased his best shot put by 10% over his best shot put at the end of 1991. By what percentage did his best shot put increase from 1990 to 1992?
(A) 10%
(B) 20%
(C) 22%
(D) 30%
(E) 32%
What’s the most obvious answer? The individual percentage gains for 1991 and 1992 were 20% and 10%, so answer choice D seems like a reasonable answer. But let’s look a little bit closer, taking this problem in two steps. What was Jordan’s shot put at the end of year 1991? A 20% increase over on 100 feet is 20 feet, so Jordan’s shot put at the end of 1991 was 120 feet. In 1992, Jordan increased his shot put by 10%. What’s 10% of 120?
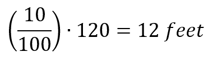
If we add 12 feet to 120 feet, we get 132 feet. From 1990 to 1992, Jordan’s shot put increased from 100 to 132, which is an increase of 32%. When percentage increases accrue over time, the overall percentage increase is more than the sum of the individual percentage gains.
The second way that the ACT likes to cloud the picture on percentage questions is to express a simple math equation with words. Let’s take a look at another question:
2. 30 percent of 350 is 50 percent of what number?
We can take these words and translate them to a math equation. If you’re unsure of how to do this, review this blog post about translating English to math. If you have worked through the words in the question correctly, you should get this:
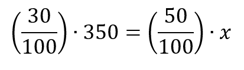
From here, this equation is pretty easy to solve:
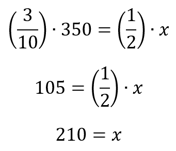
On percentage questions on the ACT Math section, remember what the true meaning of percentage is and carefully work through each part of the question, implementing the rules for translating English to Math.
For more tips, download our guide to the 6 skills you need to master for the ACT.
Need more individualized advice?
The recommendations above are general suggestions. If you have specific questions about your individual test prep plans, reach out to our experts here. We’re happy to help in any way we can.
Related Posts
How To Solve Systems of Linear Equations on the SAT & ACT Math Sections
How To Answer Trigonometry Questions on the ACT Math Section





