The SAT Math section is notoriously algebra-heavy, and many of the more frequently occurring algebra questions involve quadratics. Quadratics appear somewhat less frequently on the ACT Math section, but having a strong understanding of how to work with these equations is still vital for success. Some students struggle with quadratics questions because they see the problems as far more complicated than they really are. In reality, most quadratics questions are designed to be solved in just a few simple steps. Quadratic questions are easy to spot because there will always be a term in which the variable is squared.
Step 1: Look for ways to use Desmos or a graphing calculator
The SAT's powerful built-in Desmos calculator is perfect for solving many quadratic questions on the SAT. If you're taking the ACT, a graphing calculator such as a TI-84 can accomplish many of the same tasks. Take, for example, the question below, which is a fairly typical SAT-style question:

To solve this question, you can simply enter the equation in Desmos or a graphing calculator and look for the x value at which the graph reaches its lowest point. You can see the graph of this function below:

In Desmos, if you click on the graph at its lowest point, the x- and y-coordinates at the minimum value of the function will appear. The question asks for the x-value at which the function reaches its minimum point, so here the answer is 1.5. Depending upon your graphing calculator, you should also be able to find the minimum value of the function, either displayed directly or in the table of values.
Desmos also works especially well for questions that ask where the graphs of two equations intersect. Often, you can simply enter the equations in Desmos and read the point of intersection directly from the graph.
Step 2: If you need to do more work, simplify the quadratic.
Of course, more challenging SAT and ACT questions will require more work than simply plugging equations into Desmos and reading off the answer. For these, you'll need a more in-depth understanding of how quadratics work. The first step for most questions involves simplifying the quadratic.
![]()
The above example is ideal because there is no coefficient in front of the squared variable and all of the numbers are on one side of the equals sign. However, test questions aren’t usually presented in such a straightforward way.
First, the squared variable might not be by itself. Instead, it might have a coefficient attached to it. In these cases, it’s best to divide the whole equation by any common factors.
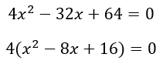
Second, the equation may not equal zero at first. Make one side of the equation equal to zero as early in the solving process as possible.
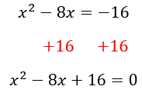
Step 3: Orient yourself.
When it comes to quadratics, there are really only two directions you can travel. Either the question will provide you with an expanded equation that you need to factor or the question will provide you with factors that you need to expand. Identifying which direction to travel is half the battle.

You should factor if a quadratic question gives you an equation and asks you to find any of the following:
- Solutions
- Roots
- Sum/difference/product/quotient of the solutions or roots
- Maximum or minimum
You should expand if the question gives you the solutions or roots and asks you to find one of these:
- An equation
- The value of a coefficient inside an equation
Step 4: Look for shortcuts.
One way to save some time on quadratic questions is to look out for perfect squares. Many quadratic questions feature perfect square trinomials that follow very predictable patterns.
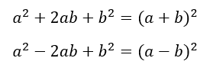
Take the following equation, for example.
![]()
The above equation includes perfect squares in the first and third terms.
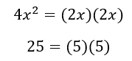
You can therefore easily factor this equation.
![]()
Even when the given equation is not a perfect square, you can still use shortcuts to solve.
![]()
Instead of reaching for a long and complicated formula to factor this equation, simply ask, “What factors of -60 add up to 11?” The answer is 15 and -4, so you can factor the equation as follows:
![]()
A final shortcut to keep in mind pertains to the roots themselves. Some word problems describe a quadratic with only one solution or one root. In these cases, use the solution to create two matching binomials and expand from there.
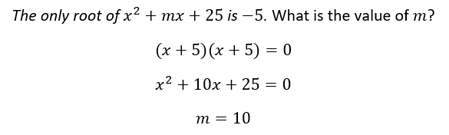
Step 4: Answer their question, not yours.
Once you’ve taken the above steps, you’re ready to solve. Just be careful to answer exactly what is asked of you. Test writers are adept at creating answer choices that solve a portion of the equation but do not answer the question itself.
Try using a step-by-step approach to solve a typical SAT quadratic question.
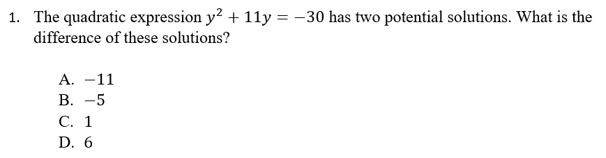
First, simplify the equation by setting the equation equal to zero.
![]()
Second, decide which direction to take your math. Will you factor or expand? The key word “solutions” appears in the question, so it looks like you’ll need to factor.
Third, check to see if you can take any shortcuts. The equation doesn’t contain any perfect squares, but there are only two factors of 30 add up to 11: five and six. You can therefore factor as follows:
![]()
Aha! Answer D shows the number 6. But wait! The question asked about the difference of the solutions. You must set each binomial equal to zero to solve for the solutions.
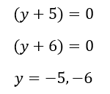
Answer B shows one of these solutions. However, recall that the question asked for the difference of the two solutions, not the solutions themselves. Therefore, the correct answer is C.
As you can see, quadratic questions are more bark than bite. With careful attention to the wording of the question and practice with the various question types, these questions can become some of the easiest math questions to solve on test day.
Need more individualized advice?
The recommendations above are general suggestions. If you have specific questions, reach out to our experts here. We’re happy to help in any way we can.
About ArborBridge
ArborBridge is the global leader in innovative, digital, one-on-one tutoring. With nearly a decade of experience teaching students online, ArborBridge supports students of all kinds: home schoolers, AP students, test preppers, and more. Our tutors specialize in creating personalized plans and in providing compassionate support for students and families.






