--- title: How to substitute numbers for variables on the ACT Math section description: "How To: Substitute Numbers for Variables on the ACT Math Section" image: https://blog.arborbridge.com/hubfs/calculator.png --- [![arb-logo@2x](https://blog.arborbridge.com/hubfs/arb-logo@2x.png)](https://www.arborbridge.com/) - [Our Services](https://arborbridge.com/our-services/) - [Academic Support](http://arborbridge.com/academic-programs/) - [SAT](https://arborbridge.com/sat/) - [ACT](https://arborbridge.com/act/) - [Subject Tests](http://arborbridge.com/subject-test/) - [AP & IB](http://arborbridge.com/ap-ib/) - [ISEE & SSAT](http://arborbridge.com/isee-ssat/) - [GRE & GMAT](http://arborbridge.com/gmat-gre-programs/) - [TOEFL](https://www.arborbridge.com/toefl-prep/) - [About Us](https://arborbridge.com/about/) - [Library](https://testprep.arborbridge.com) - [Pricing](https://www.arborbridge.com/tutoring-pricing/) - [Academic Pricing](https://www.arborbridge.com/academic-pricing/) - [SAT Pricing](https://www.arborbridge.com/sat-pricing/) - [ACT Pricing](https://www.arborbridge.com/act-pricing/) - [Subject Test Pricing](https://www.arborbridge.com/subject-test-pricing/) - [AP & IB Pricing](https://www.arborbridge.com/ap-ib-pricing/) - [ISEE & SSAT Pricing](https://www.arborbridge.com/isee-ssat-pricing/) - [GRE & GMAT Pricing](https://www.arborbridge.com/gre-gmat-pricing/) - [TOEFL Pricing](https://www.arborbridge.com/toefl-pricing/) - [Contact Us](https://arborbridge.com/contact-us/) # How to substitute numbers for variables on the ACT Math section ![ArborBridge](https://blog.arborbridge.com/hubfs/ArborBridge_Resource_Library/Branding/AB_Leaf_200x200.jpg) by [ArborBridge](https://blog.arborbridge.com/author/arborbridge) May 04, 2017 ![](https://blog.arborbridge.com/hubfs/calculator.png) If you’re like most students, you’d prefer to do math with numbers than with variables. This first time you heard “x plus 3” in your pre-algebra class, you probably said “how exactly am I supposed to add a number and a letter together?!” The ACT likes to throw variables at you in problems where they aren’t really necessary. While it is important for all students to eventually become comfortable using variables, there are some instances in which it can be easier to simply replace variables with numbers. We call this technique “pick trick.” Let’s jump right in by looking at a sample problem.   At the local supermarket, *b* boxes of apples cost *d* dollars.  Each box has *g* apples in it.  In terms of *b, d, g,* and *h¸* how many dollars does it cost to buy *h* apples total? 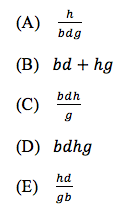![Screen Shot 2017-05-04 at 12.31.35 PM](https://blog.arborbridge.com/hs-fs/hubfs/Imported_Blog_Media/Screen-Shot-2017-05-04-at-12_31_35-PM-7.png?width=128&height=214&name=Screen-Shot-2017-05-04-at-12_31_35-PM-7.png)   Woah! I don’t know about you, but I’ve never gone to the supermarket and asked for “h apples.” Let’s make this problem a little easier. Our first step here is going to be to substitute a number for each variable. I’m going to try to pick numbers that seem realistic for this real-life problem. Let’s go with this:   *b *= 3     *d *= 12     *g* = 5      *h *= 55   The second step is to re-write the original question using these numbers. Here’s the new question: At the local supermarket, 3 boxes of apples cost 12 dollars. Each box has 5 apples in it. How many dollars does it cost you to buy 55 apples? That sounds like a much more manageable problem! Our third step is to simply work through the new problem as if we had been given those numbers in the first place. Let’s do that. If 3 boxes of apples cost 12 dollars, that’s **$4 per box**. If you want to buy 55 apples, and each box has 5 apples in it, you’ll need 11 boxes of apples. At $4 per box, that’s a total of **44 dollars**. That’s our answer! Of course, our answer choices are still in terms of the four variables we were given. Our last step is to evaluate all five answer choices (using the values we chose for each variable) and find the answer choice that matches 44 dollars.   ![Pick Trick Problem_2](https://blog.arborbridge.com/hs-fs/hubfs/Imported_Blog_Media/Pick-Trick-Problem_2-7.png?width=353&height=233&name=Pick-Trick-Problem_2-7.png)   That was pretty easy, wasn't it? The great thing about the pick trick technique is that you’ll get the correct answer no matter what numbers you plug in. There was nothing special about choosing 3, 12, 5, and 55. You could have chosen completely different numbers and still reached the same answer. You would have had a different “aim” than 44 dollars, but whatever number you ended up getting, it would be answer choice E that matched. Of course, there are certain numbers that are inherently easier than others. You probably noticed how 12 was easily divisible by 3 and that 55 was easily divisible by 5. Consistently choosing numbers that make the math easier is something that comes through practicing this technique over time. If you’d like, go ahead and try the pick trick technique on this problem using your own numbers. Then, look for ways to apply it on your next set of ACT practice problems. I’m willing to bet there will be a few instances where it’s a big help! ###### Related Posts [How To: Translate Wordy Problems from English to Math Equations](https://www.arborbridge.com/how-to-translate-wordy-problems-english-math-act-math-section/) [How To: Identify Relevant Geometry Equations](https://www.arborbridge.com/how-to-identify-relevant-geometry-equations-act-math/) --- ##### **Join ArborBridge’s Weekly News Flash and get tips like these and more delivered straight to your inbox!** - ![](https://blog.arborbridge.com/hubfs/2020%20Assets/images/print.svg) - [![](https://blog.arborbridge.com/hubfs/2020%20Assets/images/facebook.svg)](https://www.addtoany.com/add_to/facebook?linkurl=https://blog.arborbridge.com/how-to-substitute-numbers-variables-act-math-section%2F&linkname=) - [![](https://blog.arborbridge.com/hubfs/2020%20Assets/images/twitter.svg)](https://www.addtoany.com/add_to/twitter?linkurl=https://blog.arborbridge.com/how-to-substitute-numbers-variables-act-math-section%2F&linkname=) - [![](https://blog.arborbridge.com/hubfs/2020%20Assets/images/linkedin.svg)](https://www.addtoany.com/add_to/linkedin?linkurl=https://blog.arborbridge.com/how-to-substitute-numbers-variables-act-math-section%2F&linkname=) ![ArborBridge](https://blog.arborbridge.com/hubfs/ArborBridge_Resource_Library/Branding/AB_Leaf_200x200.jpg) #### About ArborBridge ArborBridge is pioneering 21st-century test prep to meet the ever-changing demands of standardized tests. We know that today’s students are digital natives. And with that in mind, every step of the way, we’ve integrated new technologies and innovative algorithms to develop the most efficient and effective one-on-one tutoring in the world. Our digital platform means we can match students with passionate, talented instructors from thousands of miles away. And whether you’re a student-athlete or the star of the school play, our highly interactive online programs empower students to prepare around even the most demanding schedules—at virtually any time of day or night. ## You also might like: [How To: Simplify Complex Sentences in the ACT English Section](https://blog.arborbridge.com/how-to-simplify-complex-sentences-act-english) [How To: Answer Statistics Questions on the ACT Math Section](https://blog.arborbridge.com/answer-statistics-questions-act-math-section) [How To: Finish Sections on Time on the ACT](https://blog.arborbridge.com/finish-sections-time-act) [![footer-logo@2x](https://blog.arborbridge.com/hubfs/2020%20Assets/images/footer-logo@2x.png)](https://www.arborbridge.com/) 100 Main Street Suite #102 Port Washington, NY 11050 (917) 525-2548 info@arborbridge.com - [Our Tutoring Services](https://www.arborbridge.com/our-services/) - [Academic Support](https://www.arborbridge.com/academic-programs/) - [SAT](https://www.arborbridge.com/sat-programs/) - [ACT](https://www.arborbridge.com/act-programs/) - [AP & IB](https://www.arborbridge.com/ap-ib-programs/) - [ISEE & SSAT](https://www.arborbridge.com/isee-ssat-programs/) - [GRE & GMAT](https://www.arborbridge.com/gmat-gre-programs/) - [TOEFL](https://www.arborbridge.com/toefl-prep/) - [About ArborBridge](https://arborbridge.com/about/) - [Library](https://testprep.arborbridge.com/) - [Pricing](https://www.arborbridge.com/tutoring-pricing/) - [Contact Us](https://arborbridge.com/contact-us/) © 2026 ArborBridge, All rights reserved. - [Terms of Use](https://blog.arborbridge.com/hubfs/termsfeed-cookies-policy-pdf-english.pdf) - [Privacy Policy](https://blog.arborbridge.com/hubfs/privacy_policy.pdf)