Geometry is like camping. Most people either absolutely love it or can’t wait to deconstruct their triangular tents and leave the woods for good. Aptly, one of the most common SAT geometry question types tests students on their knowledge of the triangle. Though the SAT can present triangles in a number of different ways, there are really only a handful of key rules you need to memorize in order to solve these questions. Let’s take a look at six important concepts:
- Angles that form a straight line always add up to 180°.
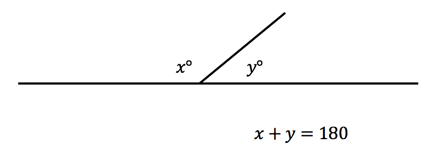
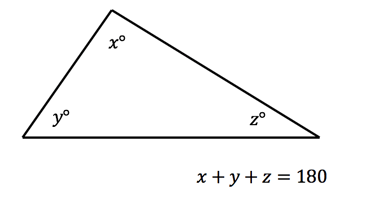
- Angles that form a triangle always add up to 180°.
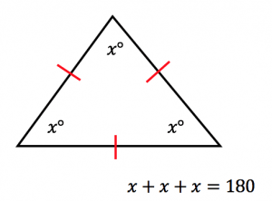
- An equilateral triangle has three equal sides and three equal angles of sixty degrees each.
Note: The lengths of each side are also equal. - An isosceles triangle has two equal sides and two equal angles.
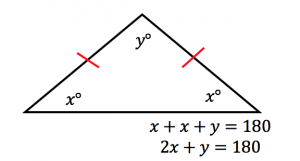
Note: The two red sides are equal, and the angles across from them are also equal. - Two parallel lines intersected by a transversal form two sets of the same four angles.
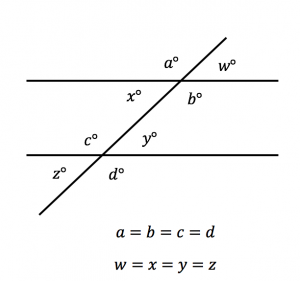
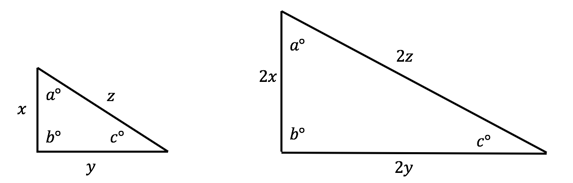
- Similar triangles have proportionate sides and equal corresponding angles.
Now that we're caught up on those ideas, let's look at the ArborBridge approach to triangle questions on the SAT math section.
Step 1: Fill out all the information.
With triangle questions, it’s usually easiest to dive right in. The moment you spot a triangle within a question, start adding in all of the missing information that you can deduce from the given information. Take this question, for example:
Automatically, we see an opportunity to fill in missing information. The angle next to 150° forms a straight line with the 150° angle. Angles that form straight lines always add up to 180°. The angle is therefore 30°. Let’s label it now.
Step 2: Use your triangle to help you solve.
At this point, we have a triangle with two of its three angles filled in. We know that angles in a triangle always add up to 180°, so the rest is simple arithmetic!
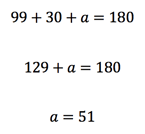
Let’s try another one.
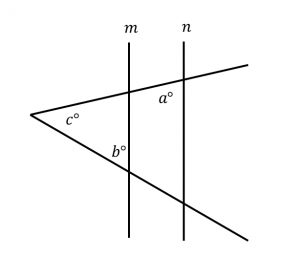
Note: Figure not drawn to scale.
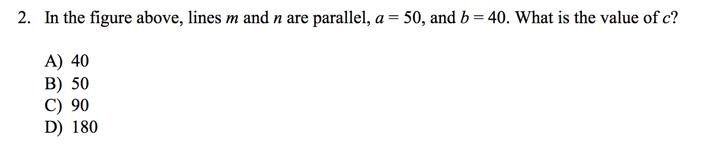
This diagram is pretty complicated. Not only is our triangle askew, but the question, itself, seems to hinge on our knowledge of parallel lines properties. Before we get too swept up in the nuances of this question, however, let’s fill in all of the information that we are given. We know that a is 50 and b is 40, so we should label that information right away.
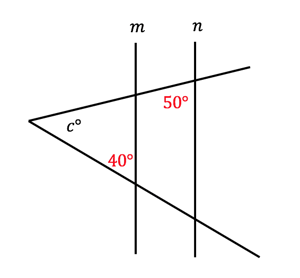
Next, let’s determine if there is any remaining hidden information to be labeled. We noted in the question that m and n are parallel. That means the lines protruding from angle c form transversals intersecting those parallel lines. Remember, when a transversal intersects two parallel lines, congruent angles are formed. Let’s zoom in on just one of the transversals to see if we can deduce what those congruent angles are.
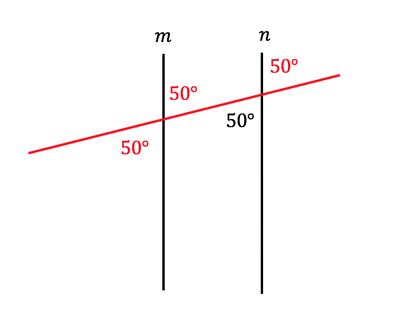
Now let’s zoom out and look at the bigger picture with all of our newfound information.
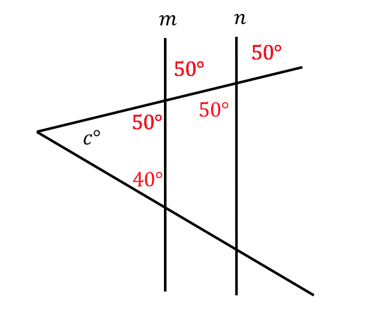
The smaller triangle containing angle c is almost complete! We know that angles in a triangle must always add up to 180°, so the rest is simple arithmetic.
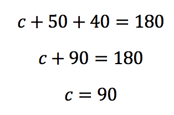
The correct answer is C.
Clearly, triangle questions aren’t always a walk in the park. However, with knowledge of a few basic geometric principles and a willingness to take each question step-by-step, you too can learn to love geometry.
For more tips, download our guide to the 6 skills you need to master for the SAT.
Need more individualized advice?
The recommendations above are general suggestions. If you have specific questions about your individual test prep plans, reach out to our experts here. We’re happy to help in any way we can.
About ArborBridge
ArborBridge is the global leader in innovative, digital, one-on-one tutoring. With nearly a decade of experience teaching students online, ArborBridge supports students of all kinds: home schoolers, AP students, test preppers, and more. Our tutors specialize in creating personalized plans and in providing compassionate support for students and families.
